class: front .pull-left-wide[ # Modelos multinivel] .pull-right-narrow[] ## Unidades en contexto ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2023 ## [.yellow[multinivel-facso.netlify.com]](https://multinivel-facso.netlify.com) ] .pull-right-narrow[ .center[ .content-block-gray[ ## Sesión 4: ## **.yellow[Correlación intra clase y estimación MLM]**] ] ] --- layout: true class: animated, fadeIn --- class: middle # - Lectura: Finch cap. 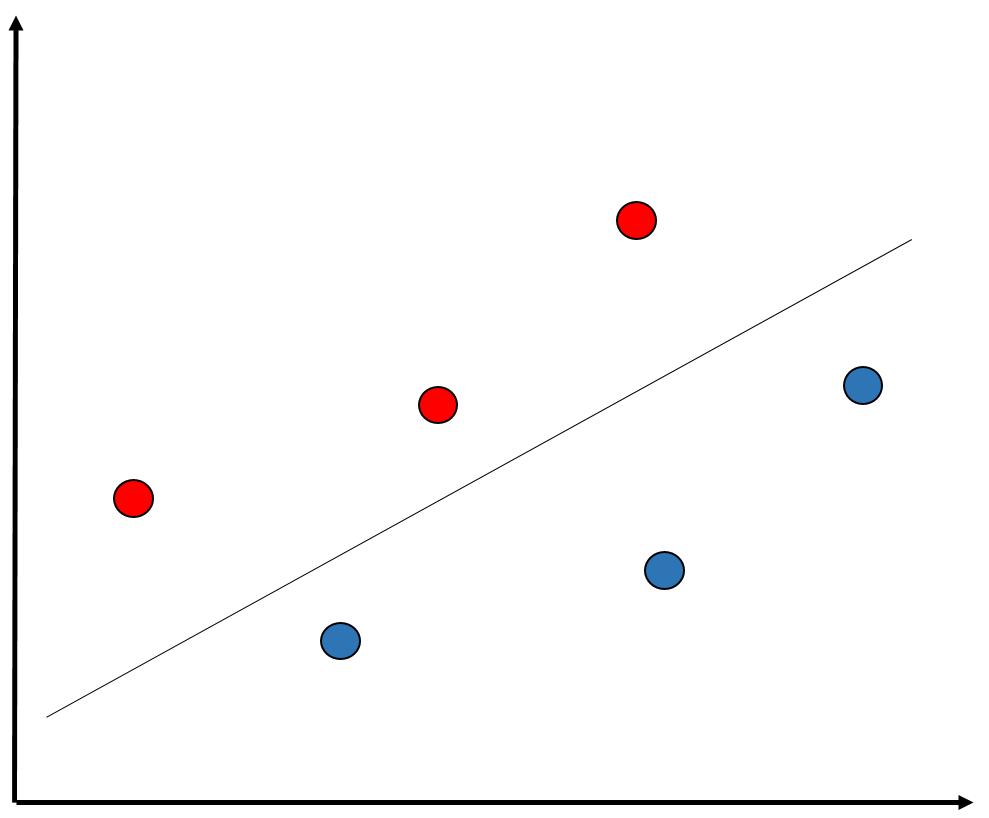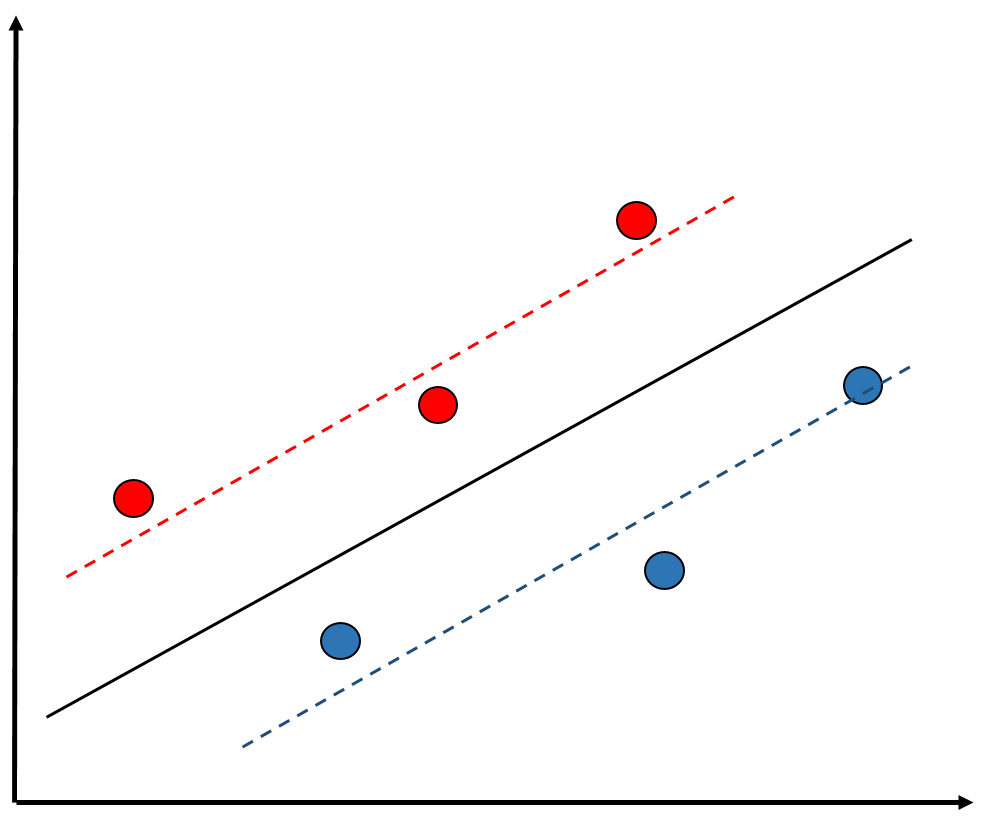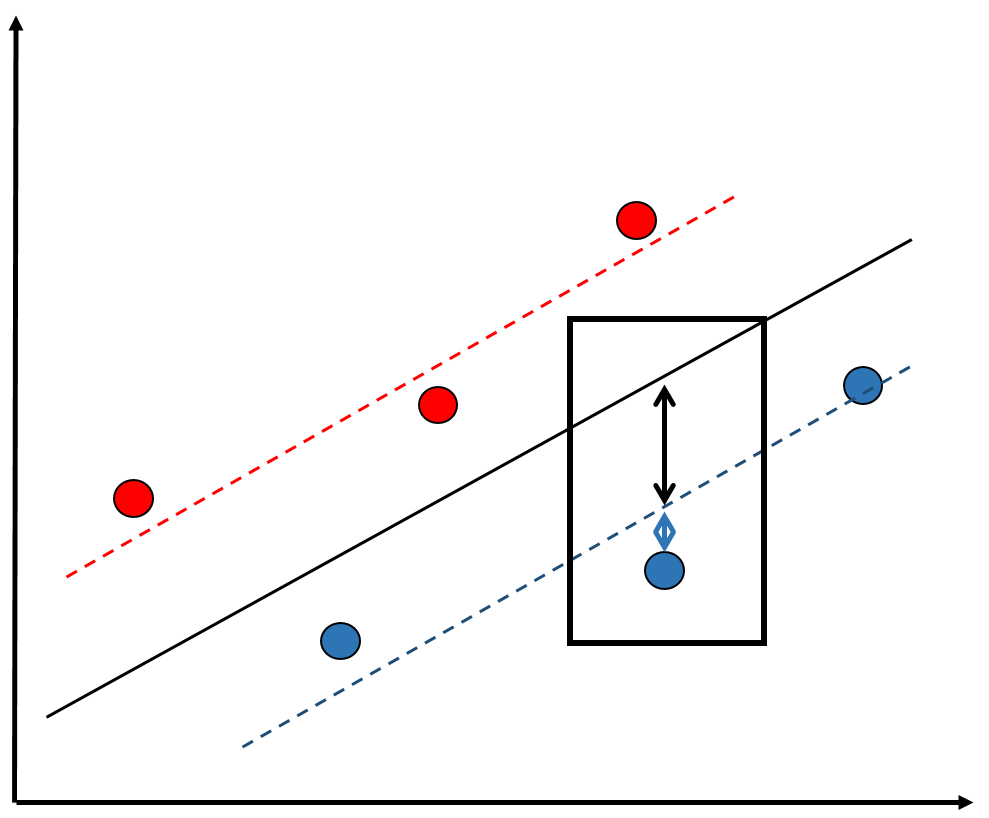3: Fitting Two-Level Models in R <br> # - Práctico --- class: roja right .pull-left-narrow[ # Contenidos ] ## .yellow[1- Resumen sesión anterior] ## 2- Modelos y pasos ## 3- Correlación intra-clase ## 4- Estimación en R --- ## Residuos y dependencia contextual  --- ## Residuos y dependencia contextual  --- ## Residuos y dependencia contextual  --- ## Modelo con coeficientes aleatorios (RCM) - Random Coefficients Models (RCM) o Mixed (effects) Models - Forma de estimación de modelos multinivel - Idea base: se agrega un parámetro *aleatorio* `\(\mu_j\)` al modelo, es decir, que posee variación en relación a unidades de nivel 2. --- ## Comparación Modelos - Modelo con datos individuales ```r reg<- lm(mathach~ses+female+sector, data=mlm) ``` - Modelo con datos agregados ```r reg_agg<- lm(mathach~ses+female+sector, data=agg_mlm) ``` --- ## Comparación Modelos .small[ ```r pacman::p_load(sjPlot,sjmisc,sjlabelled) tab_model(reg, reg_agg, show.ci=F, show.se = T, dv.labels = c("Individual", "Agregado")) ``` <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; text-align:left; "> </th> <th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Individual</th> <th colspan="3" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Agregado</th> </tr> <tr> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; text-align:left; ">Predictors</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">p</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">Estimates</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">std. Error</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; col7">p</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">12.52</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.13</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong><0.001</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">13.13</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.35</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"><strong><0.001</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">ses</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">2.88</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.10</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong><0.001</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">5.19</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.37</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"><strong><0.001</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">female</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-1.40</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.15</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong><0.001</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">-1.97</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.56</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"><strong>0.001</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">sector</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">1.96</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.15</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong><0.001</strong></td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">1.25</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.31</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; col7"><strong><0.001</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">7185</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="3">160</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">R<sup>2</sup> / R<sup>2</sup> adjusted</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.160 / 0.159</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="3">0.675 / 0.668</td> </tr> </table> ] --- ## Implicancias estimación individual/agregada - diferencias entre los coeficientes: riesgo de falacia ecológica / individualista - inflación de errores estándar para variables nivel 1 estimadas como agregadas, ej: female agregado (riesgo error tipo II) - contracción de errores estándar para variables nivel 2 estimadas como individuales, ej: sector individual (error tipo I) --- class: middle ## Alternativa: # Modelo que ajuste errores estándar según el tipo de variable nivel 1 y nivel 2 # = MULTINIVEL --- class: roja right .pull-left-narrow[ # Contenidos ] ## 1- Resumen sesión anterior ## 2- .yellow[Modelos y pasos] ## 3- Correlación intra-clase ## 4- Estimación en R --- # Pasos (usuales) en la estimación del modelo 0 Modelo nulo 1. Modelo con variables individuales 2. Modelo con variables contextuales 3. Modelo con variables individuales y contextuales 4. Modelo con pendiente (individual) aleatoria 5. 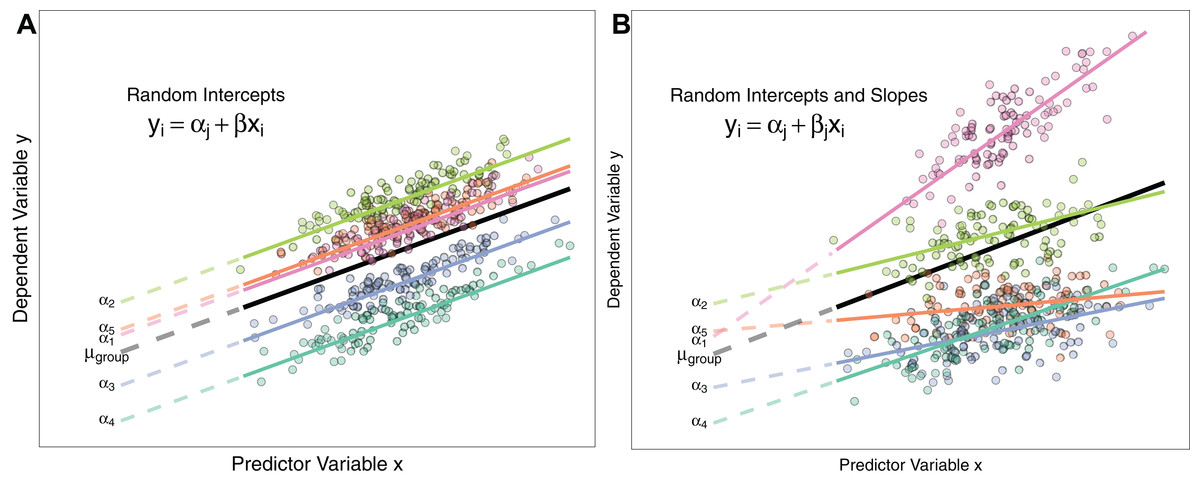Modelo con variables individuales, contextuales e interacción entre niveles (cross-level interaction) --- ## 0.Modelo nulo  --- ## 1.Modelo con variable independiente individual  --- ## 2.Modelo con variable independiente grupal  --- ## 3.Modelo con variable independiente individual y grupal  --- ## 4.Modelo con pendiente aleatoria  --- ## 4.Modelo con pendiente aleatoria  --- ## 5.Modelo con interacción entre niveles  --- ## 5.Modelo con interacción entre niveles "La relación entre X e Y varía entre contextos, y esta variación se asocia a una característica del contexto" - *Ej*: la influencia del nivel socioeconómico en rendimiento en lenguaje es moderada por la presencia de bibliotecas en las escuelas --- class: roja right .pull-left-narrow[ # Contenidos ] ## 1- Resumen sesión anterior ## 2- Modelos y pasos ## 3- .yellow[Correlación intra-clase] ## 4- Estimación en R --- class: roja, middle, center # ¿Qué problema puede haber al estimar un mismo modelo para variables individuales y agregadas? --- ## Parámetros  --- # Descomposición de la varianza Idea base de modelos multinivel: .red[la varianza de la variable dependiente se puede descomponer en distintos niveles]: - varianza Nivel 1: dentro o "within", en relación al promedio individual - varianza Nivel 2: entre o "between", en relación al promedio de los grupos - varianza Nivel `\(j\)` ... 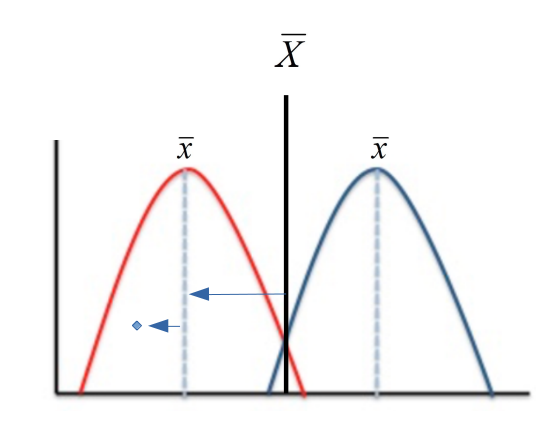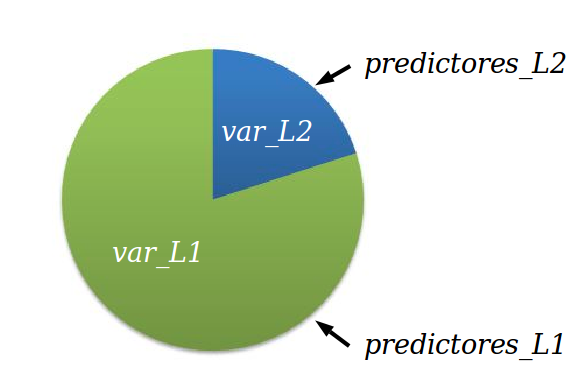--- .pull-left-narrow[# Descomposición de la varianza ] .pull-right-wide[  `$$var_{tot}=var_{dentro}+var_{entre}$$` ] --- class: middle .pull-left-narrow[ # Varianzas y predictores]  --- # Componentes de la varianza - Los efectos aleatorios asumen una varianza (estimada) en base a una distribución normal - Permiten calcular la correlación intra-clase y distintas medidas de ajuste de los modelos --- # Componentes de la varianza - `\(var \ r_{ij}=\sigma^2\)` (varianza residuos nivel individual) - `\(var \ \mu_{0j}= \tau_{00} = \tau_0^2\)` (varianza asociada a intercepto aleatorio) - `\(var \ \mu_{1j}= \tau_{11} = \tau_1^2\)` (varianza asociada a pendiente aleatoria) - `\(cov (\tau_{00},\tau_{11})= \tau_{01}\)` (covarianza entre intercepto y pendiente) --- # Componentes de la varianza  --- # 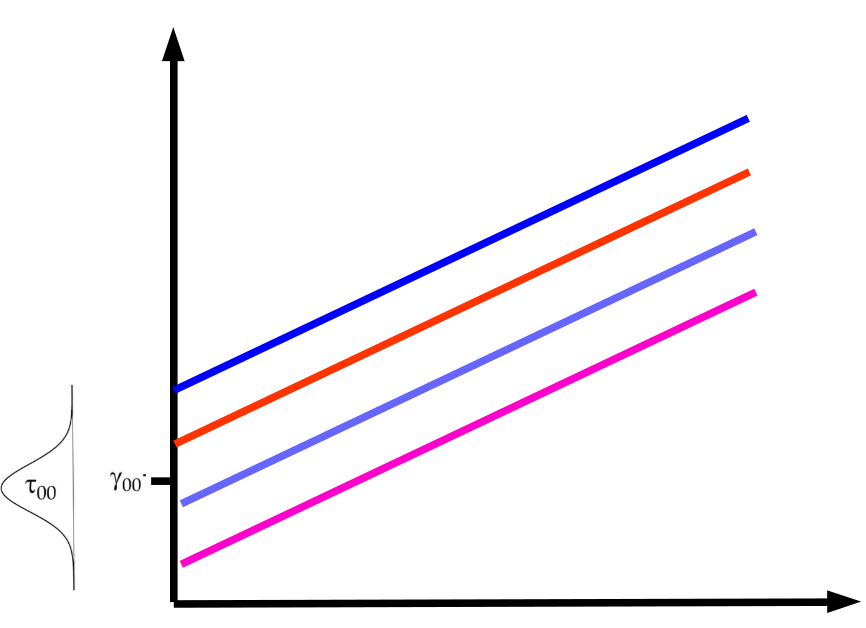Componentes de la varianza  --- ## 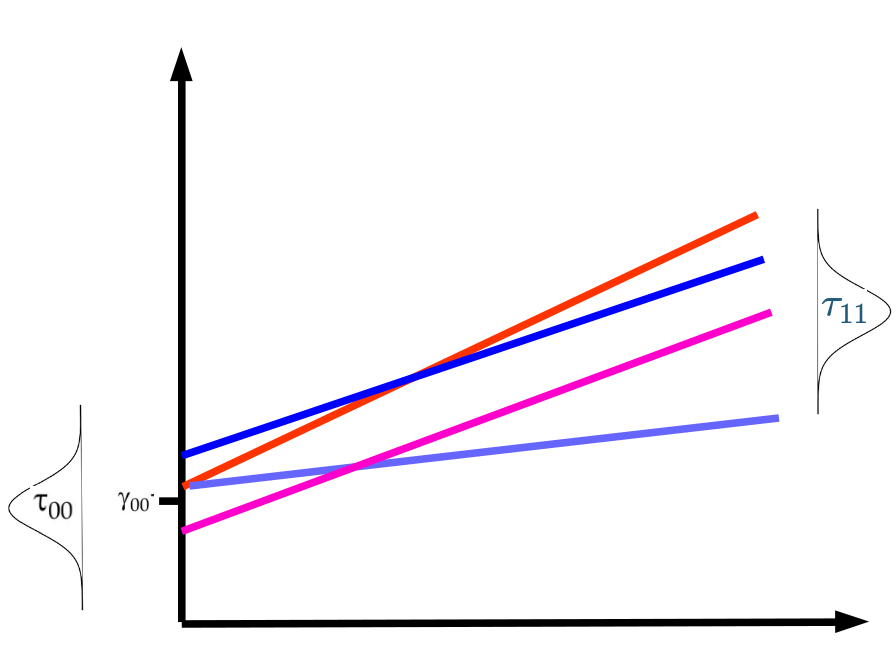Correlación intra clase: ICC - La correlación intra-clase ( `\(\rho\)` ) indica qué porcentaje de la varianza de la variable dependiente se debe a pertenencia a unidades de nivel 2 - Descomposición de la varianza en modelo nulo= `\(Var\ y=\tau_{00} + \sigma^2\)` - Es decir, parte de la varianza se debe a los individuos ( `\(\sigma^2\)` ) y parte al grupo ( `\(\tau_{00}\)` ) --- ## Correlación intra clase: ICC - Correlación intra-clase = ICC = # `$$\rho=\frac{\tau_{00}}{\tau_{00}+\sigma^2}$$` - Una ICC **baja** indica baja variabilidad de la variable dependiente entre unidades de nivel 2, y por lo tanto, menores posibilidades de dar cuenta (*explicar*) de esa varianza con predictores de nivel 2. --- class: roja, middle, center # Correlación intra-clase ## "Proporción de la varianza de la variable dependiente que se asocia a la pertenencia a unidades de nivel 2" --- class: roja right .pull-left-narrow[ # Contenidos ] ## 1- Resumen sesión anterior ## 2- Modelos y pasos ## 3- Correlación intra-clase ## 4- .yellow[Estimación en R] --- # librería lme4 - función lmer (linear mixed effects) - forma general: - `objeto <- lmer (depvar ~ predictor_1 + predictor_2 + predictor_n + (1 | cluster), data=data)` - el objeto contiene la información de la estimación; para ver un resumen, `summary(objeto)`, y de manera más presentable,`screenreg(objeto)` --- # Ejemplo Estimación en R ## -> Práctica --- class: front .pull-left-wide[ # Modelos multinivel] .pull-right-narrow[] ## Unidades en contexto ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2023 ## [.yellow[multinivel-facso.netlify.com]](https://multinivel-facso.netlify.com) ] .pull-right-narrow[ .center[ ] ]