class: front .pull-left-wide[ # Modelos multinivel] .pull-right-narrow[] ## Unidades en contexto ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2025 ## [.yellow[multinivel-facso.netlify.app]](multinivel-facso.netlify.app) ] .pull-right-narrow[ .center[ .content-block-gray[ ## Sesión 2: # **.white[Regresión]**] ] ] --- layout: true class: animated, fadeIn --- class: inverse background-image: "images/universe.jpeg" En un principio, había varianza ... --- class: roja, bottom # 1. Varianza, covarianza y correlación --- .pull-left-narrow[ # Dispersión: ## Varianza ] .pull-right-wide[ 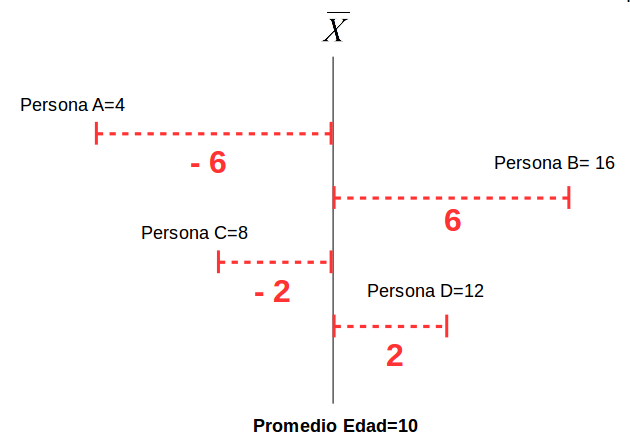 ] --- # Dispersión 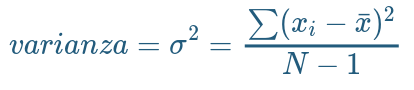 --- # Varianza & desviación estándar .pull-left[ .small[ | ID | Pje (x) | `$$x-\bar{x}$$` | `$$(x-\bar{x})^{2}$$` | |------|---------|----------|-----------| | 1 | 6 | 0.4 | 0.16 | | 2 | 4 | -1.6 | 2.56 | | 3 | 7 | 1.4 | 1.96 | | 4 | 2 | -3.6 | 12.96 | | 5 | 9 | 3.4 | 11.56 | | Sum | 28 | 0 | 29.2 | | Prom | 5.6 | | | ] ] .pull-right[ `\begin{align*} Varianza =\sigma^{2} &={\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}\over {N - 1}}\\ \sigma^{2} &={(29.2)\over {5 - 1}}\\ \sigma^{2} &= 7.3 \\ Desv.est=\sigma &=\sqrt(7.3) \\ \sigma &= 2,7 \end{align*}` ] --- # Asociación: covarianza / correlación .pull-left[ _¿Se relaciona la variación de una variable, con la variación de otra variable?_ ] -- .pull-right[ .center[] ] --- # Asociación: covarianza / correlación (II) `\begin{align*} Covarianza = cov(x,y) &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1}\\ \\ Correlación=r &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {(n-1)\sigma_x \sigma_y }\\ \\ alternativamente=r &= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}} \end{align*}` --- .pull-left-narrow[ .left[ ### Ejemplo de correlación `\(r= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}}\)` `$$=\frac{-63}{\sqrt{210*68}}$$` `$$=-0.5272$$` ] ] .pull-right-wide[ .tiny[ <br> | id| x | y | (A) `$$x-\bar{x}$$` | (B) `$$y-\bar{y}$$` | A*B | `$$(x-\bar{x})^{2}$$` | `$$(y-\bar{y})^{2}$$` | |---:|---:|---:|--------:|--------:|---------:|---------:|---------:| | 1 | 17 | 24 | -3 | 3 | -9 | 9 | 9 | | 2 | 19 | 23 | -1 | 2 | -2 | 1 | 4 | | 3 | 14 | 22 | -6 | 1 | -6 | 36 | 1 | | 4 | 22 | 17 | 2 | -4 | -8 | 4 | 16 | | 5 | 15 | 23 | -5 | 2 | -10 | 25 | 4 | | 6 | 26 | 21 | 6 | 0 | 0 | 36 | 0 | | 7 | 23 | 18 | 3 | -3 | -9 | 9 | 9 | | 8 | 21 | 17 | 1 | -4 | -4 | 1 | 16 | | 9 | 28 | 21 | 8 | 0 | 0 | 64 | 0 | | 10 | 15 | 24 | -5 | 3 | -15 | 25 | 9 | | **Sum** | | | | | -63 | 210 | 68 | | Prom | 20 | 21 | | | | | | ] ] --- # Nube de puntos (scatterplot) y correlación .center[ 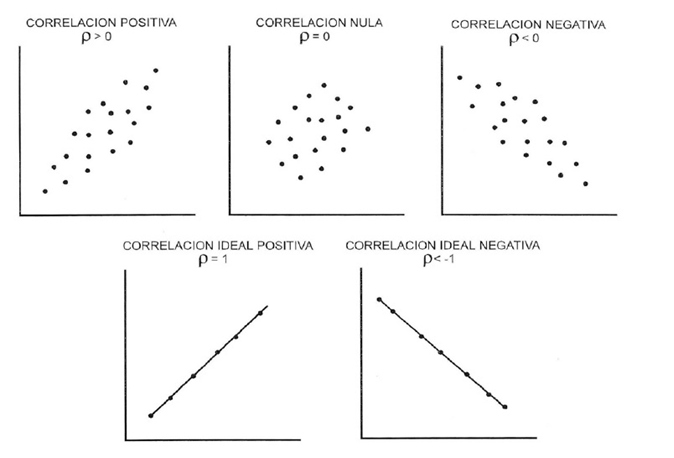 ] --- class: roja, bottom # 2. Modelo de regresión simple --- .pull-left-narrow[  ] .pull-right-wide[ - Galton: "regresión" hacia el promedio de estatura - 1886: "Regression towards mediocrity in hereditary stature", Journal of the Anthropological Institute. - Pearson: desarrollo del modelo estadístico de regresión - 1903: "Mathematical Contributions to the Theory of Evolution" ] --- # Objetivos centrales del modelo de regresión: 1. **Conocer**: la variación de la variable dependiente de acuerdo a la variación de otra(s) variable(s) independiente(s) 2. **Predecir**: estimar el valor de una variable (dependiente) de acuerdo al valor de otra(s) 3. **Inferir**: Establecer en que medida esta asociación es estadísticamente significativa --- # Objetivos centrales del modelo de regresión: Ejemplo 1. *Conocer*: Ej: En qué medida el puntaje PSU influye en el éxito académico en la universidad? -- 2. *Predecir*: Ej: Si una persona obtiene 600 puntos en la PSU, que promedio de notas en la universidad es probable que obtenga? (Atención: predicción no implica explicación) -- 3. *Inferir*: ¿Se puede generalizar a la población? ¿Con qué nivel de confianza? --- # Terminología variables .center[] --- # Ejemplo ### _¿En qué medida la experiencia previa jugando un juego predice el número de puntos obtenidos (en juego posterior)?_ .center[] --- .left-column[ # Datos ] .pull-left-narrow[  ] .pull-right[ .small[ <div class="plotly html-widget html-fill-item" id="htmlwidget-9499cbb02d9a03a5d20d" style="width:396px;height:396px;"></div> <script type="application/json" data-for="htmlwidget-9499cbb02d9a03a5d20d">{"x":{"data":[{"x":[0,0,1,1,1,2,2,2,2,3,3,3,3,3,4,4,4,4,5,5,5,6,6],"y":[2,3,2,3,4,2,3,4,5,2,3,4,5,6,3,4,5,6,4,5,6,5,6],"text":["juegos_x: 0<br />puntos_y: 2","juegos_x: 0<br />puntos_y: 3","juegos_x: 1<br />puntos_y: 2","juegos_x: 1<br />puntos_y: 3","juegos_x: 1<br />puntos_y: 4","juegos_x: 2<br />puntos_y: 2","juegos_x: 2<br />puntos_y: 3","juegos_x: 2<br />puntos_y: 4","juegos_x: 2<br />puntos_y: 5","juegos_x: 3<br />puntos_y: 2","juegos_x: 3<br />puntos_y: 3","juegos_x: 3<br />puntos_y: 4","juegos_x: 3<br />puntos_y: 5","juegos_x: 3<br />puntos_y: 6","juegos_x: 4<br />puntos_y: 3","juegos_x: 4<br />puntos_y: 4","juegos_x: 4<br />puntos_y: 5","juegos_x: 4<br />puntos_y: 6","juegos_x: 5<br />puntos_y: 4","juegos_x: 5<br />puntos_y: 5","juegos_x: 5<br />puntos_y: 6","juegos_x: 6<br />puntos_y: 5","juegos_x: 6<br />puntos_y: 6"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(0,0,0,1)","opacity":1,"size":5.6692913385826778,"symbol":"circle","line":{"width":1.8897637795275593,"color":"rgba(0,0,0,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"visible":false,"showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":23.305936073059364,"r":7.3059360730593621,"b":37.260273972602747,"l":31.415525114155255},"plot_bgcolor":"rgba(235,235,235,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.611872146118724},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.30000000000000004,6.2999999999999998],"tickmode":"array","ticktext":["0","1","2","3","4","5","6"],"tickvals":[0,1,1.9999999999999998,3,4,5,6],"categoryorder":"array","categoryarray":["0","1","2","3","4","5","6"],"nticks":null,"ticks":"outside","tickcolor":"rgba(51,51,51,1)","ticklen":3.6529680365296811,"tickwidth":0.66417600664176002,"showticklabels":true,"tickfont":{"color":"rgba(77,77,77,1)","family":"","size":11.68949771689498},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":0.66417600664176002,"zeroline":false,"anchor":"y","title":{"text":"juegos_x","font":{"color":"rgba(0,0,0,1)","family":"","size":14.611872146118724}},"scaleanchor":"y","scaleratio":1,"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.35000000000000003,7.3499999999999996],"tickmode":"array","ticktext":["0","1","2","3","4","5","6"],"tickvals":[0,1,2,3,3.9999999999999996,5,6],"categoryorder":"array","categoryarray":["0","1","2","3","4","5","6"],"nticks":null,"ticks":"outside","tickcolor":"rgba(51,51,51,1)","ticklen":3.6529680365296811,"tickwidth":0.66417600664176002,"showticklabels":true,"tickfont":{"color":"rgba(77,77,77,1)","family":"","size":11.68949771689498},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":0.66417600664176002,"zeroline":false,"anchor":"x","title":{"text":"puntos_y","font":{"color":"rgba(0,0,0,1)","family":"","size":14.611872146118724}},"scaleanchor":"x","scaleratio":1,"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.8897637795275593,"font":{"color":"rgba(0,0,0,1)","family":"","size":11.68949771689498}},"hovermode":"closest","barmode":"relative"},"config":{"doubleClick":"reset","modeBarButtonsToAdd":["hoverclosest","hovercompare"],"showSendToCloud":false},"source":"A","attrs":{"2034c0676bd9fd":{"x":{},"y":{},"type":"scatter"},"2034c047f7d7f5":{"x":{},"y":{}}},"cur_data":"2034c0676bd9fd","visdat":{"2034c0676bd9fd":["function (y) ","x"],"2034c047f7d7f5":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.20000000000000001,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> ] ] --- # Descriptivos <table style="text-align:center"><tr><td colspan="6" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Statistic</td><td>N</td><td>Mean</td><td>St. Dev.</td><td>Min</td><td>Max</td></tr> <tr><td colspan="6" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">id</td><td>23</td><td>12.000</td><td>6.782</td><td>1</td><td>23</td></tr> <tr><td style="text-align:left">juegos_x</td><td>23</td><td>3.000</td><td>1.758</td><td>0</td><td>6</td></tr> <tr><td style="text-align:left">puntos_y</td><td>23</td><td>4.000</td><td>1.382</td><td>2</td><td>6</td></tr> <tr><td colspan="6" style="border-bottom: 1px solid black"></td></tr></table> --- .left-column[ # **Medias condicionales** ] .center[] ??? Ejemplo para los sujetos con 1 en X hay 3 valores de Y: 2, 3 y 4. Por lo tanto, la media condicional de Y dado X=1 es 3 --- .left-column[ # Idea de distribución condicional ] .center[] --- .left-column[ # La recta de regresión ] .right-column[ .center[] .small[ La (co) variación general de Y respecto a X se puede expresar en una ecuación de la recta = **modelo de regresión** ] ] --- class: inverse, right ## Para obtener la “mejor recta” se utiliza la estimación de mínimos cuadrados (EMC, o **OLS** – Ordinary Least Squares) -- ## OLS minimiza la suma de los **residuos** = distancias entre las observaciones y la recta en el eje vertical --- # Componentes de la ecuación de la recta de regresión `$$\widehat{Y}=b_{0} +b_{1}X$$` Donde - `\(\widehat{Y}\)` es el valor estimado de `\(Y\)` - `\(b_{0}\)` es el intercepto de la recta (el valor de Y cuando X es 0) - `\(b_{1}\)` es el coeficiente de regresión, que nos dice cuánto aumenta Y por cada punto que aumenta X --- # Estimación de los coeficientes de la ecuación: `$$b_{1}=\frac{Cov(XY)}{VarX}$$` `$$b_{1}=\frac{\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1}}{\frac{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} {n-1}}$$` Y simplificando `$$b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}$$` --- # Estimación de los coeficientes de la ecuación: Luego despejando el valor de `\(b_{0}\)` `$$b_{0}=\bar{Y}-b_{1}\bar{X}$$` --- # Cálculo de coeficientes La base para todos estos calculos es la diferencia de cada valor menos su promedio. Para ello: 1. Vamos a crear los siguientes vectores (variables) en nuestra base de datos `$$difx=x-\bar{x}$$` `$$dify=y-\bar{y}$$` --- # Cálculo basado en el ejemplo 2.Con la información anterior podemos obtener la diferencia de productos cruzados `$$difcru=(x-\bar{x})*(y-\bar{y})$$` 3.También obtenemos las diferencias del promedio al cuadrado de X= `$$difx2=(x-\bar{x})^2$$` --- count: false .panel1-ejemplo-auto[ ``` r *datos_b <-datos datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y ## 1 1 0 2 ## 2 2 0 3 ## 3 3 1 2 ## 4 4 1 3 ## 5 5 1 4 ## 6 6 2 2 ## 7 7 2 3 ## 8 8 2 4 ## 9 9 2 5 ## 10 10 3 2 ## 11 11 3 3 ## 12 12 3 4 ## 13 13 3 5 ## 14 14 3 6 ## 15 15 4 3 ## 16 16 4 4 ## 17 17 4 5 ## 18 18 4 6 ## 19 19 5 4 ## 20 20 5 5 ## 21 21 5 6 ## 22 22 6 5 ## 23 23 6 6 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos *datos$p_x <- mean(datos$juegos_x) datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y ## 1 1 0 2 ## 2 2 0 3 ## 3 3 1 2 ## 4 4 1 3 ## 5 5 1 4 ## 6 6 2 2 ## 7 7 2 3 ## 8 8 2 4 ## 9 9 2 5 ## 10 10 3 2 ## 11 11 3 3 ## 12 12 3 4 ## 13 13 3 5 ## 14 14 3 6 ## 15 15 4 3 ## 16 16 4 4 ## 17 17 4 5 ## 18 18 4 6 ## 19 19 5 4 ## 20 20 5 5 ## 21 21 5 6 ## 22 22 6 5 ## 23 23 6 6 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos datos$p_x <- mean(datos$juegos_x) *datos$difx <-datos$juegos_x-datos$p_x datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y p_x ## 1 1 0 2 3 ## 2 2 0 3 3 ## 3 3 1 2 3 ## 4 4 1 3 3 ## 5 5 1 4 3 ## 6 6 2 2 3 ## 7 7 2 3 3 ## 8 8 2 4 3 ## 9 9 2 5 3 ## 10 10 3 2 3 ## 11 11 3 3 3 ## 12 12 3 4 3 ## 13 13 3 5 3 ## 14 14 3 6 3 ## 15 15 4 3 3 ## 16 16 4 4 3 ## 17 17 4 5 3 ## 18 18 4 6 3 ## 19 19 5 4 3 ## 20 20 5 5 3 ## 21 21 5 6 3 ## 22 22 6 5 3 ## 23 23 6 6 3 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x *datos$p_y <- mean(datos$puntos_y) datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y p_x difx ## 1 1 0 2 3 -3 ## 2 2 0 3 3 -3 ## 3 3 1 2 3 -2 ## 4 4 1 3 3 -2 ## 5 5 1 4 3 -2 ## 6 6 2 2 3 -1 ## 7 7 2 3 3 -1 ## 8 8 2 4 3 -1 ## 9 9 2 5 3 -1 ## 10 10 3 2 3 0 ## 11 11 3 3 3 0 ## 12 12 3 4 3 0 ## 13 13 3 5 3 0 ## 14 14 3 6 3 0 ## 15 15 4 3 3 1 ## 16 16 4 4 3 1 ## 17 17 4 5 3 1 ## 18 18 4 6 3 1 ## 19 19 5 4 3 2 ## 20 20 5 5 3 2 ## 21 21 5 6 3 2 ## 22 22 6 5 3 3 ## 23 23 6 6 3 3 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) *datos$dify <-datos$puntos_y-datos$p_y datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y p_x difx p_y ## 1 1 0 2 3 -3 4 ## 2 2 0 3 3 -3 4 ## 3 3 1 2 3 -2 4 ## 4 4 1 3 3 -2 4 ## 5 5 1 4 3 -2 4 ## 6 6 2 2 3 -1 4 ## 7 7 2 3 3 -1 4 ## 8 8 2 4 3 -1 4 ## 9 9 2 5 3 -1 4 ## 10 10 3 2 3 0 4 ## 11 11 3 3 3 0 4 ## 12 12 3 4 3 0 4 ## 13 13 3 5 3 0 4 ## 14 14 3 6 3 0 4 ## 15 15 4 3 3 1 4 ## 16 16 4 4 3 1 4 ## 17 17 4 5 3 1 4 ## 18 18 4 6 3 1 4 ## 19 19 5 4 3 2 4 ## 20 20 5 5 3 2 4 ## 21 21 5 6 3 2 4 ## 22 22 6 5 3 3 4 ## 23 23 6 6 3 3 4 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) datos$dify <-datos$puntos_y-datos$p_y *datos$dif_cru <-datos$difx*datos$dify datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y p_x difx p_y dify ## 1 1 0 2 3 -3 4 -2 ## 2 2 0 3 3 -3 4 -1 ## 3 3 1 2 3 -2 4 -2 ## 4 4 1 3 3 -2 4 -1 ## 5 5 1 4 3 -2 4 0 ## 6 6 2 2 3 -1 4 -2 ## 7 7 2 3 3 -1 4 -1 ## 8 8 2 4 3 -1 4 0 ## 9 9 2 5 3 -1 4 1 ## 10 10 3 2 3 0 4 -2 ## 11 11 3 3 3 0 4 -1 ## 12 12 3 4 3 0 4 0 ## 13 13 3 5 3 0 4 1 ## 14 14 3 6 3 0 4 2 ## 15 15 4 3 3 1 4 -1 ## 16 16 4 4 3 1 4 0 ## 17 17 4 5 3 1 4 1 ## 18 18 4 6 3 1 4 2 ## 19 19 5 4 3 2 4 0 ## 20 20 5 5 3 2 4 1 ## 21 21 5 6 3 2 4 2 ## 22 22 6 5 3 3 4 1 ## 23 23 6 6 3 3 4 2 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) datos$dify <-datos$puntos_y-datos$p_y datos$dif_cru <-datos$difx*datos$dify *datos$difx2 <-datos$difx^2 datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y p_x difx p_y dify dif_cru ## 1 1 0 2 3 -3 4 -2 6 ## 2 2 0 3 3 -3 4 -1 3 ## 3 3 1 2 3 -2 4 -2 4 ## 4 4 1 3 3 -2 4 -1 2 ## 5 5 1 4 3 -2 4 0 0 ## 6 6 2 2 3 -1 4 -2 2 ## 7 7 2 3 3 -1 4 -1 1 ## 8 8 2 4 3 -1 4 0 0 ## 9 9 2 5 3 -1 4 1 -1 ## 10 10 3 2 3 0 4 -2 0 ## 11 11 3 3 3 0 4 -1 0 ## 12 12 3 4 3 0 4 0 0 ## 13 13 3 5 3 0 4 1 0 ## 14 14 3 6 3 0 4 2 0 ## 15 15 4 3 3 1 4 -1 -1 ## 16 16 4 4 3 1 4 0 0 ## 17 17 4 5 3 1 4 1 1 ## 18 18 4 6 3 1 4 2 2 ## 19 19 5 4 3 2 4 0 0 ## 20 20 5 5 3 2 4 1 2 ## 21 21 5 6 3 2 4 2 4 ## 22 22 6 5 3 3 4 1 3 ## 23 23 6 6 3 3 4 2 6 ``` ] --- count: false .panel1-ejemplo-auto[ ``` r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) datos$dify <-datos$puntos_y-datos$p_y datos$dif_cru <-datos$difx*datos$dify datos$difx2 <-datos$difx^2 *datos$difx2 <-datos$difx^2 datos_b ``` ] .panel2-ejemplo-auto[ ``` ## id juegos_x puntos_y p_x difx p_y dify dif_cru difx2 ## 1 1 0 2 3 -3 4 -2 6 9 ## 2 2 0 3 3 -3 4 -1 3 9 ## 3 3 1 2 3 -2 4 -2 4 4 ## 4 4 1 3 3 -2 4 -1 2 4 ## 5 5 1 4 3 -2 4 0 0 4 ## 6 6 2 2 3 -1 4 -2 2 1 ## 7 7 2 3 3 -1 4 -1 1 1 ## 8 8 2 4 3 -1 4 0 0 1 ## 9 9 2 5 3 -1 4 1 -1 1 ## 10 10 3 2 3 0 4 -2 0 0 ## 11 11 3 3 3 0 4 -1 0 0 ## 12 12 3 4 3 0 4 0 0 0 ## 13 13 3 5 3 0 4 1 0 0 ## 14 14 3 6 3 0 4 2 0 0 ## 15 15 4 3 3 1 4 -1 -1 1 ## 16 16 4 4 3 1 4 0 0 1 ## 17 17 4 5 3 1 4 1 1 1 ## 18 18 4 6 3 1 4 2 2 1 ## 19 19 5 4 3 2 4 0 0 4 ## 20 20 5 5 3 2 4 1 2 4 ## 21 21 5 6 3 2 4 2 4 4 ## 22 22 6 5 3 3 4 1 3 9 ## 23 23 6 6 3 3 4 2 6 9 ``` ] <style> .panel1-ejemplo-auto { color: black; width: 38.6060606060606%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-ejemplo-auto { color: black; width: 59.3939393939394%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-ejemplo-auto { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- # Cálculo basado en el ejemplo Y con esto podemos obtener la suma de productos cruzados y la suma de cuadrados de X ``` ## [1] 34 ``` ``` ## [1] 68 ``` --- # Reemplazando en la fórmula `$$b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}=\frac{34}{68}=0.5$$` --- # Cálculo basado en el ejemplo Reemplazando podemos obtener el valor de `\(b_{0}\)` `$$b_{0}=\bar{Y}-b_{1}\bar{X}$$` `$$b_{0}=4-(3 * 0.5)=2.5$$` Completando la ecuación: `$$\widehat{Y}=2.5+0.5X$$` Por cada unidad que aumenta la experiencia en juego (x), los puntos obtenidos(y) aumentan en 0.5. --- # Cálculo basado en el ejemplo `$$\widehat{Y}=2.5+0.5X$$` Esto nos permite estimar el valor de `\(Y\)` (o su media condicional) basado en el puntaje `\(X\)`. Por ejemplo, cuál es el valor estimado de `\(Y\)` dado `\(X=3\)`? `$$\widehat{Y}=2.5+(0.5*3)$$` `$$\widehat{Y}=2.5+(3*0.5)=4$$` El valor estimado de puntos para una persona que ha jugado 3 veces es 4. --- .left-column[ ## Cálculo basado en el ejemplo ] .small[ .center[ <!-- --> ] ] --- class: inverse middle right # Por cada punto que aumenta X, Y aumenta en `\(\beta\)` ---- (tatuar) --- class: roja, bottom, right # 3. Ajuste y residuos --- .pull-left-wide[  ] .pull-right-narrow[ <br> # El cuarteto de Anscombe (1973) .small[ Podemos tener un mismo modelo de regresión para relaciones distintas entre datos ] ] --- # ¿Qué tan bueno es nuestro modelo? - El cálculo del `\(\beta\)` busca minimizar los residuos (de ahí "mínimos cuadrados ordinarios") -- - Una vez minimizados los residuos, se puede evaluar el ajuste - qué tan bien representa nuestro modelo la realidad - cuánto error (de predicción) estamos cometiendo con nuestro modelo --- class: inverse, right ## Un modelo es mejor mientras **mejor refleje** lo que sucede con los datos -- ## En otras palabras, cuando se parece o **ajusta** mejor a los datos -- ## ... y en otras: cuando los **residuos** son menores --- # Observado, estimado & residuo .pull-left-wide[  ] .pull-right-narrow[ - observado: `\(Y\)` - estimado: `\(\widehat{Y}\)` - residuo: `\(Y-\widehat{Y}\)` ] --- # Varianza explicada de Y ¿Qué parte de la varianza de ingreso (Y) se asocia a educación? .center[] --- # Varianza explicada de Y: `\(R^2\)` - ¿Cuánto de los ingresos puedo predecir con educación (regresión) y cuánto me estoy equivocando (residuos)? -- - el `\(R^2\)` - es la proporción de la varianza de Y que se asocia a X - varía entre 0 y 1, y se puede expresar en porcentaje -- - Entonces, podemos descomponer la varianza de Y en 2: aquella asociada a X (regresión) y la que no se asocia a X (residuos) --- # ¿Cómo se calcula el `\(R^2\)`? - para saber qué porcentaje de `\(Y\)` se asocia a `\(X\)` vamos a considerar los siguientes valores de `\(Y\)`: `\(Y\)` = Valor observado de Y `\(\widehat{Y}\)` = estimación de Y a partir de X `\(\bar{Y}\)` = promedio de Y --- # Descomponiendo Y Conceptualmente: `$$SS_{tot}=SS_{reg} + SS_{error}$$` .center[  ] --- .pull-left-wide[ ] .pull-right-narrow[ .right[ ## Descomponiendo Y ]] .pull-left-wide[ `$$Y=\bar{Y}+(\widehat{Y}-\bar{Y}) + (Y-\widehat{Y})$$` $$ \Sigma(y_i - \bar{y})^2=\Sigma (\hat{y}_i-\bar{y})^2 +\Sigma(y_i-\hat{y}_i)^2$$ ] --- # Varianza explicada Por lo tanto: `$$SS_{tot}=SS_{reg} + SS_{error}$$` -- `$$\frac{SS_{tot}}{SS_{tot}}=\frac{SS_{reg}}{SS_{tot}} + \frac{SS_{error}}{SS_{tot}}$$` -- `$$1=\frac{SS_{reg}}{SS_{tot}}+\frac{SS_{error}}{SS_{tot}}$$` `$$\frac{SS_{reg}}{SS_{tot}}= 1- \frac{SS_{error}}{SS_{tot}}=R^2$$` --- .pull-left[ ## Una parte de la variación de Y se relaciona con la variación de X: `\(R^2\)` ] .pull-right[  ] --- # Sobre relación entre correlación y regresión (simple) - La correlación entre X e Y es la misma que entre Y e X - peeero: La regresión entre X e Y **no** es la misma que entre Y y X -- - Correlación de Pearson al cuadrado ( `\(r^2\)` ) es `\(R^2\)` -- - La correlación equivale al beta de regresión simple estandarizado --- class: roja bottom right # Regresión múltiple --- # Regresión simple .center[  ] `$$\widehat{Y}=\beta_{0} +\beta_{1}X_{1}$$` - Modelo con pretensiones explicativas: cambios en Y en base a X (predictor) --- # ¿Qué pasa cuando hay más de un predictor/hipótesis? .center[  ] - --- # ¿Qué pasa cuando hay más de un predictor/hipótesis? .center[  ] `$$\widehat{Y}=\beta_{0} +\beta_{1}X_{1} + \beta_{2}X_{2}+ \beta_{3}X_{3} + \beta_{i}X_{i}$$` --- class: inverse, middle, center .large[ # El modelo de regresión es un modelo .red[SUMATIVO] ] <br> `$$\widehat{Y}=\beta_{0} +\beta_{1}X_{1} + \beta_{2}X_{2}+ \beta_{3}X_{3} + \beta_{i}X_{i}$$` --- class: inverse, center # entonces ... ¿simplemente agregar más predictores al modelo? .medium[ `$$\widehat{ingreso}=\beta_{0} +\beta_{1}educación + \beta_{2}edad+ \beta_{3}género + ... + \beta_{i}X_{i}$$` ] -- # si, .red[pero ...] --- # Posibilidad de predictores correlacionados .center[  ] -- .center[ .red[¿Qué implicancias puede tener para la estimación la correlación entre predictores? ]] --- # Agregando predictores al modelo .pull-left[ .center[] `$$\widehat{Ingreso}=b_0+b_1(Educ)$$` ] -- .pull-right[ .center[] `$$\widehat{Ingreso}=b_0+b_1(Educ)+b_2(Int)$$` ] ??? - Tenemos un modelo teórico que relaciona ingreso con nivel educacional: a mayor ingreso, mayor nivel educacional. - Esto puede expresarse en un modelo de regresión - Qué sucede si nos surge la pregunta sobre la posibilidad de que otras variables también tienen que ver con ingreso? - Se puede agregar una tercera variable al modelo, pero: ¿qué consecuencias teóricas y empíricas tiene esto? --- # Agregando predictores al modelo .pull-left-narrow[ .center[] ] .pull-right-wide[ - Teóricamente el modelo asume covariación entre Ingreso y Educación, y entre _Ingreso_ e _Inteligencia_ {{content}} ] -- - Pero ... también existe la posibilidad de covariación entre los predictores _Educación_ e _Inteligencia_ {{content}} -- - Para poder sumar el efecto neto de cada predictor se debe **controlar** la covariación entre predictores --- class:roja # La regresión múltiple no es equivalente a regresiones simples estimadas por separado con distintos predictores --- class: inverse, middle, center # .large[.yellow[Concepto de .red[control]]] --- .pull-left-narrow[ # 1. Control por diseño <br>  ] .pull-right-wide[ - Característico de la metodología experimental {{content}} ] -- - El control se logra por diseño mediante **aleatorización** (distribución al azar) de sujetos a diferentes situaciones experimentales, generando **grupos equivalentes** {{content}} -- - La aleatorización intenta aislar el **efecto del tratamiento** de todas las otras variables que podrían afectar en la respuesta ] --- ## 2. Control estadístico - En datos observacionales de encuestas en general no hay control por diseño, por lo que se recurre al **control estadístico** -- - En el **modelo de regresión** se logra incluyendo predictores que teóricamente podrían dar cuenta o afectar la relación entre X e Y. -- - La inclusión de **otros predictores** despeja o "controla" la asociación de `\(X_1\)` e `\(Y\)`, aislando el efecto conjunto de `\(X_1\)` y `\(X_2\)` (... y `\(X_n\)`) --- .pull-left-wide[ ## Control estadístico - ¿Qué efecto posee el nivel educacional en ingreso, _controlando por_ inteligencia? ] .pull-right-narrow[  ] ---- **Conceptualmente:** .small[ - aislar el efecto de educación en ingreso, manteniendo la inteligencia _constante_. - estimar el efecto de educación en ingreso independiente del efecto de la inteligencia - estimación del efecto de educación en ingreso _ceteris paribus_ (manteniendo el efecto del resto de los predictores constante) ] --- class: inverse, center, middle, exclude # POR LO TANTO ## Un aspecto **central** en regresión múltiple, tanto conceptual como estadísticamente, tiene que ver con el .yellow[control de la CORRELACION] ENTRE .red[PREDICTORES] O VARIABLES INDEPENDIENTES (X) --- ### Simulación 1: sin correlación relevante entre predictores .pull-left-narrow[ .center[] ] -- .pull-right_wide[.small[ <!-- --> ] ] --- ### Simulación 1: sin correlación relevante entre predictores .small[ <table class="texreg" style="margin: 10px auto;border-collapse: collapse;border-spacing: 0px;caption-side: bottom;color: #000000;border-top: 2px solid #000000;"> <caption> </caption> <thead> <tr> <th style="padding-left: 5px;padding-right: 5px;"> </th> <th style="padding-left: 5px;padding-right: 5px;">Model 1</th> <th style="padding-left: 5px;padding-right: 5px;">Model 2</th> <th style="padding-left: 5px;padding-right: 5px;">Model 3</th> </tr> </thead> <tbody> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">(Intercept)</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.16</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">educacion</td> <td style="padding-left: 5px;padding-right: 5px;">0.40<sup>***</sup></td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.40<sup>***</sup></td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">inteligencia</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.30<sup>**</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.31<sup>**</sup></td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> </tr> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.13</td> <td style="padding-left: 5px;padding-right: 5px;">0.08</td> <td style="padding-left: 5px;padding-right: 5px;">0.21</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">Adj. R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.12</td> <td style="padding-left: 5px;padding-right: 5px;">0.07</td> <td style="padding-left: 5px;padding-right: 5px;">0.20</td> </tr> <tr style="border-bottom: 2px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">Num. obs.</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> </tr> </tbody> <tfoot> <tr> <td style="font-size: 0.8em;" colspan="4"><sup>***</sup>p < 0.001; <sup>**</sup>p < 0.01; <sup>*</sup>p < 0.05</td> </tr> </tfoot> </table> ] --- ### Simulación 2: con correlación entre predictores .pull-left-narrow[ .center[] ] -- .pull-right-wide[.medium[ <!-- --> ] ] --- ### Simulación 2: con correlación entre predictores .small[ <table class="texreg" style="margin: 10px auto;border-collapse: collapse;border-spacing: 0px;caption-side: bottom;color: #000000;border-top: 2px solid #000000;"> <caption> </caption> <thead> <tr> <th style="padding-left: 5px;padding-right: 5px;"> </th> <th style="padding-left: 5px;padding-right: 5px;">Model 1</th> <th style="padding-left: 5px;padding-right: 5px;">Model 2</th> <th style="padding-left: 5px;padding-right: 5px;">Model 3</th> </tr> </thead> <tbody> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">(Intercept)</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.16</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">educacion</td> <td style="padding-left: 5px;padding-right: 5px;">0.40<sup>***</sup></td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.35<sup>**</sup></td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.11)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">inteligencia</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.30<sup>**</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.18</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.11)</td> </tr> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.13</td> <td style="padding-left: 5px;padding-right: 5px;">0.08</td> <td style="padding-left: 5px;padding-right: 5px;">0.16</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">Adj. R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.12</td> <td style="padding-left: 5px;padding-right: 5px;">0.07</td> <td style="padding-left: 5px;padding-right: 5px;">0.14</td> </tr> <tr style="border-bottom: 2px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">Num. obs.</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> </tr> </tbody> <tfoot> <tr> <td style="font-size: 0.8em;" colspan="4"><sup>***</sup>p < 0.001; <sup>**</sup>p < 0.01; <sup>*</sup>p < 0.05</td> </tr> </tfoot> </table> ] --- ## Comparando .pull-left[ .small[ <table class="texreg" style="margin: 10px auto;border-collapse: collapse;border-spacing: 0px;caption-side: bottom;color: #000000;border-top: 2px solid #000000;"> <caption> </caption> <thead> <tr> <th style="padding-left: 5px;padding-right: 5px;"> </th> <th style="padding-left: 5px;padding-right: 5px;">Model 1</th> <th style="padding-left: 5px;padding-right: 5px;">Model 2</th> <th style="padding-left: 5px;padding-right: 5px;">Model 3</th> </tr> </thead> <tbody> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">(Intercept)</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.16</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">educacion</td> <td style="padding-left: 5px;padding-right: 5px;">0.40<sup>***</sup></td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.40<sup>***</sup></td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">inteligencia</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.30<sup>**</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.31<sup>**</sup></td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> </tr> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.13</td> <td style="padding-left: 5px;padding-right: 5px;">0.08</td> <td style="padding-left: 5px;padding-right: 5px;">0.21</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">Adj. R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.12</td> <td style="padding-left: 5px;padding-right: 5px;">0.07</td> <td style="padding-left: 5px;padding-right: 5px;">0.20</td> </tr> <tr style="border-bottom: 2px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">Num. obs.</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> </tr> </tbody> <tfoot> <tr> <td style="font-size: 0.8em;" colspan="4"><sup>***</sup>p < 0.001; <sup>**</sup>p < 0.01; <sup>*</sup>p < 0.05</td> </tr> </tfoot> </table> ] ] .pull-right[ .small[ <table class="texreg" style="margin: 10px auto;border-collapse: collapse;border-spacing: 0px;caption-side: bottom;color: #000000;border-top: 2px solid #000000;"> <caption> </caption> <thead> <tr> <th style="padding-left: 5px;padding-right: 5px;"> </th> <th style="padding-left: 5px;padding-right: 5px;">Model 1</th> <th style="padding-left: 5px;padding-right: 5px;">Model 2</th> <th style="padding-left: 5px;padding-right: 5px;">Model 3</th> </tr> </thead> <tbody> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">(Intercept)</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.15</td> <td style="padding-left: 5px;padding-right: 5px;">-0.16</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.09)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">educacion</td> <td style="padding-left: 5px;padding-right: 5px;">0.40<sup>***</sup></td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.35<sup>**</sup></td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.11)</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">inteligencia</td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">0.30<sup>**</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.18</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;"> </td> <td style="padding-left: 5px;padding-right: 5px;">(0.10)</td> <td style="padding-left: 5px;padding-right: 5px;">(0.11)</td> </tr> <tr style="border-top: 1px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.13</td> <td style="padding-left: 5px;padding-right: 5px;">0.08</td> <td style="padding-left: 5px;padding-right: 5px;">0.16</td> </tr> <tr> <td style="padding-left: 5px;padding-right: 5px;">Adj. R<sup>2</sup></td> <td style="padding-left: 5px;padding-right: 5px;">0.12</td> <td style="padding-left: 5px;padding-right: 5px;">0.07</td> <td style="padding-left: 5px;padding-right: 5px;">0.14</td> </tr> <tr style="border-bottom: 2px solid #000000;"> <td style="padding-left: 5px;padding-right: 5px;">Num. obs.</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> <td style="padding-left: 5px;padding-right: 5px;">100</td> </tr> </tbody> <tfoot> <tr> <td style="font-size: 0.8em;" colspan="4"><sup>***</sup>p < 0.001; <sup>**</sup>p < 0.01; <sup>*</sup>p < 0.05</td> </tr> </tfoot> </table> ] ] --- # Estimación de parámetros y control estadístico - Los coeficientes de regresión `\(\beta\)` no alteran su valor en los modelos en ausencia de correlación entre predictores `\(X\)` (Ejemplo 1) -- - Si hay correlación entre predictores, el valor de los coeficientes de regresión será distinto en modelos simples y en modelos múltiples -> **control estadístico** -- - Por ello, en regresión múltiple se habla de coeficientes de regresión **parciales** --- # Estimación de parámetros y control estadístico - Ejemplo 2, modelo 3: El ingreso aumenta en 0.4 puntos por cada nivel adicional de educación, **controlando por inteligencia**. O también ... - manteniendo la inteligencia _constante_ - _ceteris paribus_ --- class: inverse ## Resumen - Regresión múltiple: más de un predictor / variable independiente en el modelo - Permite - contrastar hipótesis de la **influencia simultánea** de más de una variable - **controlar** por la posible influencia de terceras variables (control estadístico) --- class: front .pull-left-wide[ # Modelos multinivel] .pull-right-narrow[] ## Unidades en contexto ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2025 ## [.yellow[multinivel-facso.netlify.app]](https://multinivel-facso.netlify.app) ] ]